Shaanxi Provincial Center for Disease Control and Prevention, Xi'an 710054, Shaanxi, China

Objective To evaluate the feasibility of time series model to predict the incidence of infectious diseases. Methods According to the time series of reported monthly incidence of bacillary dysentery in Shaanxi province from 2004 to 2012, the autoregressive integrated moving average (ARIMA) model was established by using the incidence data of bacillary dysentery from January to December 2013 as demonstration data. The predictive power of ARIMA model was evaluated. Results The case curve is not only with a long-term descending trend but also with annual seasonality. The relative optimum fitting model was ARIMA(0,1,1)×(1,1,0)₁₂. Ljung-Box Q had no statistical significance (Ljung-Box Q=21.994,P=0.143) and residuals was the white noise. The average of the relative error between actual value and predicted value from January to December in 2013 was 20.75% (maximum 40.37%, minimum 4.94%). Conclusion The ARIMA model can be used to effectively predict the incidence of bacillary dysentery in Shaanxi. More original data are needed in order to optimize the model.

Keywords:    Bacillary dysentery   Monthly incidence   Autoregressive integrated moving average moded  

陕西省疾病预防控制中心信息科, 陕西 西安 710054

收稿日期：2014-3-27

通讯作者：郁会莲，Tel：029-82210356，Email：QL12@163.com

目的 探讨时间序列模型预测传染性疾病发病率的可行性，应用自回归移动平均（autoregressive integrated moving average，ARIMA）模型对陕西省细菌性痢疾进行预测，为制定细菌性痢疾防治策略提供依据。 方法 根据2004-2012年陕西省细菌性痢疾月报告发病率的时间序列，以2013年1 12月的月发病率作为验证数据，建立ARIMA模型，并对预测效果进行评价。 结果 陕西省2004-2012年细菌性痢疾月发病率即含有长期递减趋势又含有以年为周期的季节效应，拟合的相对最佳模型为ARIMA（0，1，1）×（1，1，0）₁₂。残差分析统计量经检验差异无统计学意义（Ljung-Box Q=21.994，P=0.143），提示残差为白噪声。2013年1 12月实际值与预测值的相对误差平均值为20.75%，最大40.37%，最小4.94%。 结论 ARIMA模型可以较好地预测陕西省细菌性痢疾的发病趋势，模型预测效果的优化有待原始数据的进一步积累。

关键词:    细菌性痢疾   月发病率   自回归移动平均模型  

1 材料与方法

1.1 资料来源

1.2 ARIMA模型分析步骤

1.2.1 时间序列分析的条件

1.2.2 模型识别

1.2.3 模型的参数估计和检验

1.2.4 模型的诊断

1.2.5 模型预测

1.3 分析软件

2 结果

2.1 序列平稳化处理

2.2 模型识别及定阶

2.3 模型参数估计与诊断

2.4 模型预测

3 讨论

细菌性痢疾是一种常见的肠道传染病，常年散发，夏秋多见，是我国的常见病、多发病。细菌性痢疾属于法定报告乙类传染病，发病率在陕西省一直位居乙类传染病第3位，近年来发病率也高于全国平均水平。本文在陕西省历年细菌性痢疾监测数据的基础上，拟采用求和自回归移动平均模型(ARIMA)建立发病预测模型，对陕西省细菌性痢疾报告发病率进行分析、预测，为预防控制工作提供参考依据。

根据中国疾病预防控制信息系统中的《疾病监测信息报告管理系统》，按照已审核状态，分别下载2004-2013年陕西省细菌性痢疾分月报告发病率，形成所需的时间序列数据库。

季节性时间序列采用乘积季节模型，即ARIMA(p,d,q)×(P,D,Q)_s。其中d为平稳化过程中差分的阶数，p、q为自回归和移动平均阶数。P、Q为季节性自回归和移动平均阶数，D为季节差分阶数，S为季节周期^[1]。ARIMA的建模步骤如下：

时间序列分析是建立在序列平稳的基础上，如果序列不满足平稳性条件，即需要对序列进行数据变换或差分，以获取平稳的时间序列。

确定模型ARIMA(p,d,q)或ARIMA(p,d,q)×(P,D,Q)_s中的参数p、d、q和P、D、Q及S。根据差分次数分别确定模型中的d和D，p、q值可由自相关函数图(ACF)和偏自相关函数图(PACF)得到^[2]。季节模型的参数P、Q阶数一般在2以内，分别取0、1、2试验，选择最佳模型^[3]。

采用极大似然法或最小二乘法估计模型参数，在各参数有统计学意义的基础上，根据拟合优度统计量比较模型的优劣。采用标准化的贝叶斯准则(BIC)比较模型的拟合优度，值较小的模型较好^[4]。

对模型的残差序列进行白噪声检验，检验方法是计算Box-Jenkins统计量(Q值)。

以2004-2012年陕西省细菌性痢疾月发病率为原始时间序列拟合ARIMA模型，预测2013年1 12月的细菌性痢疾月发病率，并根据预测值与实际值的相对误差判断模型的预测效果。

采用SPSS 17.0软件进行ARIMA模型分析，通过Date命令建立时间序列，运用Analyze命令观察数据的平稳性和建立模型。

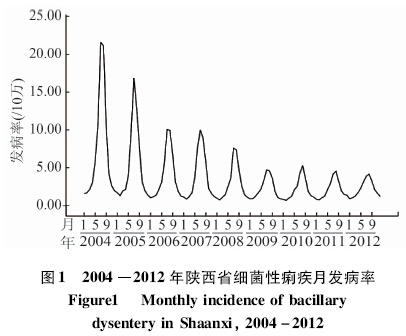
绘制2004年1月至2012年12月的细菌性痢疾月发病率的曲线图(图1)，发现细菌性痢疾月发病率总体上呈明显的下降趋势，每年7月至8月为发病高峰期，显示出明显的非平稳性特征，具有长期趋势和季节性周期性。

图1 2004-2012年陕西省细菌性痢疾月发病率
Figure 1 Monthly incidence of bacillary dysentery in Shaanxi, 2004-2012

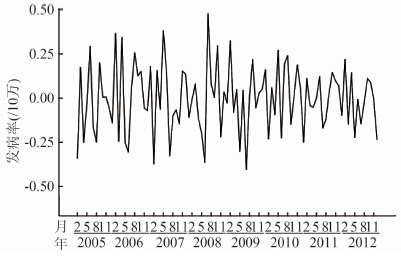
对原始数据采取自然对数转换、一阶差分和一次季节差分，消除序列的长期趋势和季节效应，差分后的时间序列图、ACF图和PACF图较平稳，同时确定ARIMA(p,d,q)×(P,D,Q)₁₂中的d和D分别为1和1，见图2～4。

图2 2004-2012年陕西省细菌性痢疾月发病率经
Figure 2 Monthly incidence of bacillary dysentery after taking differences of lag1, lag12 and nature log in Shaanxi, 2004-2012

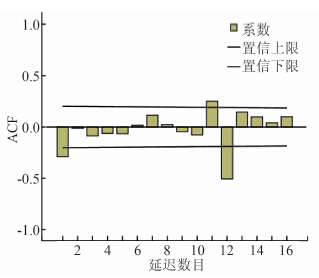
图3 2004-2012年陕西省细菌性痢疾月发病率
Figure 3 ACF of monthly incidence of bacillary dysentery after tranquilization in Shaanxi, 2004-2012

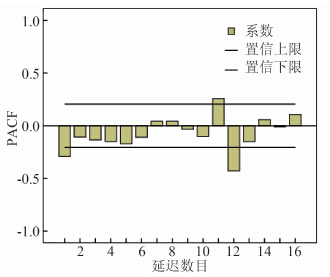
图4 2004-2012年陕西省细菌性痢疾月发病率
Figure 4 PACF of monthly incidence of bacillary dysentery after tranquilization in Shaanxi, 2004-2012

根据差分变换的次数，可初步确定模型应是以12个月为周期的复合季节模型ARIMA(p,1,q)×(P,1,Q)₁₂。自相关分析图(ACF图和PACF图)是将时间序列的自相关系数与偏自相关系数绘制成图，并标出一定的可信区间。利用自相关分析图可以分析时间序列的随机性、平稳性和季节性。差分后的ACF图和PACF图显示，当lag=1时，ACF值和PACF值都超出了可信区间，显示了负向的低谷，提示该序列在一阶以内相关性较大。当lag>1时，其后的ACF值迅速衰减，并接近于0，提示ACF值截尾且相关性较小；PACF值衰减较为缓慢，提示出现拖尾且相关性逐渐减小。参照几种常见ARIMA模型自相关分析标准图^[2]，可初步确定p=0，q=1。在lag=12时， ACF值和PACF值显示明显超出95%可信区间，这提示此处相关性较大，还需对季节模型的参数进行分析。对季节模型参数P,Q的识别，分别取0、1、2逐个试验^[3]，根据模型的拟合优度、残差情况以及系数间的相关性进行综合判断。

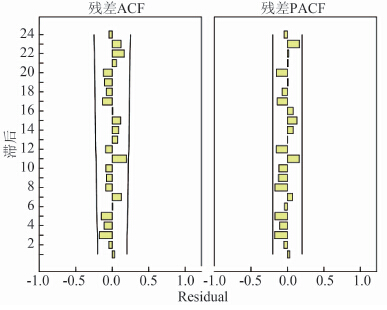
参数估计、模型拟合优度统计量指标选择平稳R²、均方根误差、BIC进行评价。通过反复试验，最终选择ARIMA(0,1,1)×(1,1,0)₁₂模型为最佳模型，正态化BIC最小(-0.224)、平稳R²=0.322、均方根误差相对较小(0.832)，其Ljung-Box Q=21.994，P=0.143，提示残差序列为白噪声。图5显示，残差序列ACF值和PACF值均落入随机区间内，提示模型信息提取比较充分，时间序列各项之间没有相关性^[4]。

图5 模型ARIMA(0,1,1)×(1,1,0)₁₂ 残差序列ACF、PACF函数图
Figure 5 ACF and PACF of residual series of ARIMA(0,1,1)×(1,1,0)₁₂

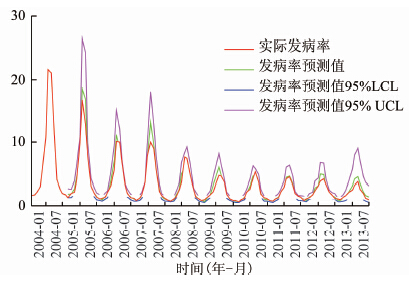
以陕西省2004-2012年细菌性痢疾月发病率时间序列拟合ARIMA(0,1,1)×(1,1,0)₁₂模型后，再以陕西省2013年1 12月细菌性痢疾月发病率为验证数据进行预测，根据预测值与实际值的相对误差判断模型的预测效果，见表1，并绘制实际值和预测值序列图，见图6。本模型从区间估计上，预测结果总体趋势与实际情况一致，实测值未超出95%可信限范围。从点估计值上，1 4月预测值低于实际值，5 12月预测值高于实际值。在预测值的精度上，2013年1 12月平均相对误差20.75%，最大40.37%，最小4.94%(相对误差%=︱预测值-真实值︱÷真实值×100%)。

图6 2004-2013年陕西省细菌性痢疾月发病率趋势预测图
Figure 6 Predication of monthly incidence of bacillary dysentery in Shaanxi, 2004-2012

表1 2013年1 12月陕西省细菌性痢疾发病率预测值
Table1  Actual and predicted monthly incidences of bacillary dysentery in Shaanxi, January-December 2013

月份	实际值 (/10万)	预测值 (/10万)	月发病率 预测值(95%CI)	相对误差 (%)
1	1.10	0.87	0.64～1.19	20.48
2	1.00	0.91	0.62～1.33	9.48
3	1.40	1.18	0.76～1.83	15.91
4	1.61	1.48	0.90～2.44	7.97
5	2.17	2.28	1.31～3.95	4.94
6	2.46	3.10	1.71～5.64	26.15
7	3.22	4.16	2.19～7.90	29.16
8	3.78	4.52	2.28～8.96	19.50
9	2.60	3.38	1.64～6.99	30.09
10	1.98	2.11	0.98～4.54	6.71
11	1.17	1.62	0.72～3.61	38.28
12	0.96	1.35	0.58～3.12	40.37
平均相对误差				20.75

在疾病特征描述性分析的基础上开展疾病流行趋势预测是疾病监测的目的之一。时间序列分析方法有很多种，而ARIMA模型是目前应用于传染病预测较多的方法之一，它是一种精度较高的时序短期预测方法^[5]。ARIMA模型的特点是以时间综合代替温度、季节、病原体变化、预防控制干预等影响因素，根据历史数据建立ARIMA模型进行外推预测，为传染病疫情研判和干预效果评价提供参考^[4,6]。

细菌性痢疾是一种急性肠道传染病，该病具有发病率高，病后免疫力持续时间较短，不同性别菌株之间无交叉免疫等特点^[3]。陕西省细菌性痢疾月发病率呈现明显的长期趋势和季节高峰，现利用历史数据，建立ARIMA模型预测其发病趋势，探讨此种预测方法的可行性。分析结果显示模型ARIMA(0,1,1)×(1,1,0)₁₂的各月细菌性痢疾发病率预测值与实际值基本一致，实际值均落入95%可信区间内，并对陕西省2013年1 12月的细菌性痢疾发病率进行预测，显现出较好的适用效果，提示ARIMA模型对陕西省细菌性痢疾月发病率进行预测具有可行性。而11、12月相对误差较大，说明预测精度有待进一步提高，且影响细菌性痢疾发病率的因素有很多，可将不断产生的新的观察值纳入模型，通过对模型的不断修正，以更好地反映真实的发病情况。

本研究显示ARIMA模型能较好地用于细菌性痢疾发病的短期预测，根据预测数据有针对性地开展防治工作，有助于提高疾病预防控制工作的能力。在疫情监测工作中，根据预测数据的可信区间，可以判断实际发病率是否在正常范围波动，传染病的发病是否为散发、是否按照既往的规律发生变化。如果实际发病率在预测值95%可信区间内波动，则表明疫情基本正常；如果超出，则表明疫情已不同于以往流行规律，应警惕传染病暴发或流行的可能性^[7-8]。对细菌性痢疾进行时间序列分析可为传染病早期预测预警模型的建立提供借鉴，从而有针对性地采取相应的预防控制措施。当然，不同的传染病有着不同的发病模式，同样，不同的预测模型也有着不同的数学理论基础和适用条件。尽管ARIMA模型的建立已有一套明确的规则，适用于各种复杂的模式^[9]，但在实际运用中仍存在弊端。没有一种数学模型可以实现对一段时间历史数据的完全拟合和预测，所以我们要在实际工作中不断发现问题、总结经验，以提高监测数据的质量；同时，加强对数学模型的研究，分析采用何种方法和模型进行预测效果更好^[10-12]。这样，才能为传染病防控工作提供更为可靠的数据和建议。

[1] Bai YF,Xu LH,Guo ZX, et al.Time series Autoregressive Intergrated Moving Average model to predict brucellosis incidence in Shaanxi province[J]. Disease Surveillance,2011,26(8):647-650.(in Chinese) 白永飞,徐丽红,郭支喜,等.山西省布鲁氏菌病时间序列自回归移动平均模型分析[J]. 疾病监测,2011,26(8):647-650.
[2] Sun ZQ.Medical Statistic[M].second edition.Beijing:Peoples Health Publishing House,2006.(in Chinese) 孙振球.医学统计学[M].2版.北京:人民卫生出版社,2006.
[3] Yang PR,Tian H,Yan CY.Application of autoregressive inte- grated moving average model in forecasting of the monyhly incidence rate in Baoji[J].Journal of Public Health and Preventive Medicine,2012,23(1):16-19.(in Chinese) 杨培荣,田辉,严钏元.自回归移动平均模型在宝鸡市细菌性痢疾月发病率预测中的应用[J].公共卫生与预防医学,2012,23(1):16-19.
[4] Huang XX,Zhang SX,Zhao JW, et al.Prediction of monthly hand foot and mouth disease incidence in China by using autoregressive integrated moving average model[J]. Disease Surveillance,2013,28(5):396-399.(in Chinese) 黄晓霞,张顺先,赵俊伟,等.采用自回归移动平均模型预测中国手足口病月发病率[J]. 疾病监测,2013,28(5):396-399.
[5] Chen C,Tian X,Zhou JH, et al.Building and application of ARIMA model on Mumps epidemic[J]. Chinese Journal of Public Health,2012,28(2):1252-253.(in Chinese) 陈超,田鑫,周剑惠,等.流行性腮腺炎疫情时间序列模型建立与应用[J].中国公共卫生,2012,28(2):252-253.
[6] Peng ZX,Bao CJ,Zhao Y, et al.ARIMA Product Season Model and its application on forecasting in incidence of infectious disease[J]. Application of Statistics and Management,2008,27(2):362-368.(in Chinese) 彭志行,鲍昌俊,赵杨,等.ARIMA乘积季节模型及其在传染病发病预测中的应用[J]. 数理统计与管理,2008,27(2):362-368.
[7] Wu JB,Ye LX,You EK.Prediction of incidence of notifiable contagious diseases by application of time series model[J].Journal of Mathematical Medicine,2007,20(1):90-92.(in Chinese) 吴家兵,叶临湘,尤尔科.ARIMA模型在传染病发病率预测中的应用[J].数理医药学杂志,2007,20(1):90-92.
[8] Wu JB,Ye LX,You EK.Application of time series model in the prediction of the incidence rate of infectious disease[J]. Chinese Journal of Health Statistics,2006,23(3):276.(in Chinese) 吴家兵,叶临湘,尤尔科.时间序列模型在传染病发病率预测中的应用[J].中国卫生统计,2006,23(3):276.
[9] Glynn PW,Sigman K.Independent sampling of a stochastic process[J].Stoch Proc Appl,1998,74:151-164.
[10] Wang J,Zhou MG,Hu J, et al.Application of ARIMA model in predicting tuberculosis incidence in Jiangxi[J]. Disease Surveillance,2012,27(6):462-467.(in Chinese) 王健,周脉耕,胡嘉,等.求和自回归移动平均模型在江西省结核病发病预测中应用[J].疾病监测,2012,27(6):462-467.
[11] Feng D,Han XN,Zhao WJ, et al.Using ARIMA model to surveillance and forecast the incidence rate of Not I fiable infectious diseases in Mainland China[J].Chinese Journal of Disease Control and Prevention,2007,11(2):140-143.(in Chinese) 冯丹,韩晓娜,赵文娟,等.中国内地法定报告传染病预测和监测的ARIMA模型[J].疾病控制杂志,2007,11(2):140-143.
[12] Yin ZD,Luo HM,Li YX, et al.The application of autoregressive integrated moving average model on the prediction of Japanese encephalitis cases[J].Chinese Journal of Vaccines and Immunization,2010,16(5):457-461.(in Chinese) 尹遵栋,罗会明,李艺星,等.时间序列分析(自回归求和移动平均模型)在流行性乙型脑炎预测中的应用[J].中国疫苗和免疫,2010,16(5):457-461.