疾病监测  2016, Vol. 31 Issue (5): 411-415

扩展功能

文章信息

赵梦娇, 于秋燕, 赵小冬, 许华茹, 徐淑慧
ZHAO Meng-jiao, YU Qiu-yan, ZHAO Xiao-dong, XU Hua-ru, XU Shu-hui
ARIMA季节乘积模型预测济南市猩红热发病趋势
Application of ARIMA model for prediction of incidence of scarlet fever
疾病监测, 2016, 31(5): 411-415
Disease Surveillance, 2016, 31(5): 411-415
10.3784/j.issn.1003-9961.2016.05.014

文章历史

收稿日期：2015-11-26
引用本文 0
赵梦娇, 于秋燕, 赵小冬, 许华茹, 徐淑慧. ARIMA季节乘积模型预测济南市猩红热发病趋势[J]. 疾病监测, 2016, 31(5): 411-415.
ZHAO Meng-jiao, YU Qiu-yan, ZHAO Xiao-dong, XU Hua-ru, XU Shu-hui. Application of ARIMA model for prediction of incidence of scarlet fever[J]. Disease Surveillance, 2016, 31(5): 411-415.
ARIMA季节乘积模型预测济南市猩红热发病趋势
赵梦娇, 于秋燕, 赵小冬, 许华茹, 徐淑慧     
济南市疾病预防控制中心, 山东 济南 250021
收稿日期: 2015-11-26
作者简介: 赵梦娇,女,山东省泰安市人,硕士,医师,主要从事传染病预防控制、突发事件监测预警、风险评估工作
作者贡献: 赵梦娇：负责整个研究设计、实施以及论文撰写
于秋燕、赵小冬、许华茹：负责数据整理、文献查阅等工作
徐淑慧：负责文章审改。
通信作者: 徐淑慧,Tel:0531-81278907,Email:xushuhui66@126.com.
摘要: 目的 探讨ARIMA季节乘积模型在济南市猩红热月发病率预测中的应用,并预测猩红热月发病趋势,为制订防控策略提供依据。 方法 对济南市2006-2014年猩红热月发病率资料建立ARIMA季节乘积模型,利用2015年1-6月发病资料检验模型的精度,并预测2015年各月发病率。 结果 构建ARIMA(1,0,0)×(0,1,1)12模型可以用于济南市猩红热月发病率的拟合和预测,模型决定系数R2=0.64。 结论 2015年济南市猩红热处于高流行期,应警惕出现流行和暴发的可能,在高发时间、高发地点做好猩红热的监测和应对工作,防止暴发流行。
关键词： 猩红热     预测     ARIMA模型    
Application of ARIMA model for prediction of incidence of scarlet fever
ZHAO Meng-jiao, YU Qiu-yan, ZHAO Xiao-dong, XU Hua-ru, XU Shu-hui     
Jinan Center for Disease Control and Prevention, Jinan 250021, Shandong, China
Abstract: Objective To evaluate the performance of multiple seasonal autoregressive integrated moving average (ARIMA) model in the prediction of scarlet fever incidence in Jinan, and provide evidence for the prevention and control of the disease. Methods The incidence data of scarlet fever in Jinan from 2006 to 2014 were used to establish ARIMA model and the incidence data in Jinan from January to June in 2015 were used to evaluate the accuracy of the model. The incidence of scarlet fever in Jinan in 2105 was predicted by using the model. Results ARIMA (1,0,0)×(0,1,1)12 model could be used to predict epidemiological tendency of scarlet fever in Jinan. The R2 of the model was 0.64. Conclusion The incidence of scarlet fever in Jinan was still at high level in 2015. It is necessary to strengthen the scarlet fever surveillance to prevent the outbreak of scarlet fever.
Key words: Scarlet fever     Prediction     ARIMA model    

猩红热为A群溶血性链球菌感染引起的急性呼吸道传染病，主要通过空气飞沫传播，冬春季多发，人群普遍易感，目前尚无针对性的疫苗。2011年以来，全国猩红热病例迅速增加[1-2],近两年，济南市猩红热高发，而对其流行规律和趋势系统的研究较少，本研究尝试利用猩红热月发病率建立预测模型，利用ARIMA季节乘积模型对济南市猩红热流行趋势进行预测。根据预测数据，较为精准的掌握济南市猩红热发病规律和趋势，为早期发现暴发流行，及时采取防控措施提供参考依据。

1 对象与方法 1.1 资料来源

猩红热发病资料来源于2006-2014年中国疾病预防控制信息系统，人口资料来源于济南市2002-2014统计年鉴，计算2006-2014年猩红热月发病率。

1.2 方法

差分自回归移动平均模型(ARIMA模型)是由Box和Jenkins提出的一种经典时间序列预测方法，将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。根据序列是否平稳和回归中所含部分的不同，分为AR模型(p)、MA模型(q)和ARIMA模型(p，d，q)。对于有季节性变动规律的序列，其季节模型为ARIMA (P，D，Q)S。ARIMA季节乘积模型表示为ARIMA (p，d，q)(P，D，Q)S。

ARIMA模型建立通常包括3个步骤:(1) 判断并处理序列平稳性。ARIMA模型需要时间序列是平稳序列，即均值和方差是平稳的，两者不随时间的变动而变动。对于不平稳的序列通常采用对数变换或差分等方法处理，使序列平稳化。(2) 模型的识别。需要根据序列特征识别模型的阶数p、d、q，可以通过自相关函数(ACF)、偏相关函数(PACF)识别模型阶数。(3) 参数估计和模型诊断。确定模型阶数后，通过非线性最小二乘法或极大似然估计法估计。建立的模型需要经过诊断，确认模型合理后才能使用，一般从3个方面进行，①残差的均值应该与0有显著差异，可以采用t检验；②残差的分布应该为正态分布，可以采用Kolmogorov-Smirnov检验；③残差序列不存在自相关，可采用Box-Ljung检验[3-4]。

1.3 统计学分析

使用Excel软件对数据进行整理、清洗和核对，计算月发病率。用Kolmogorov-Smirnov检验对残差分布进行正态检验，用Box-Ljung检验进行白噪声检验，Augmented Dickey-Fuller test statistic检验数据平稳性，显著性水准取P=0.05。使用Eviews 8.0软件进行单位根检验，用SPSS 20.0软件对数据建立拟合ARIMA模型，并进行预测。

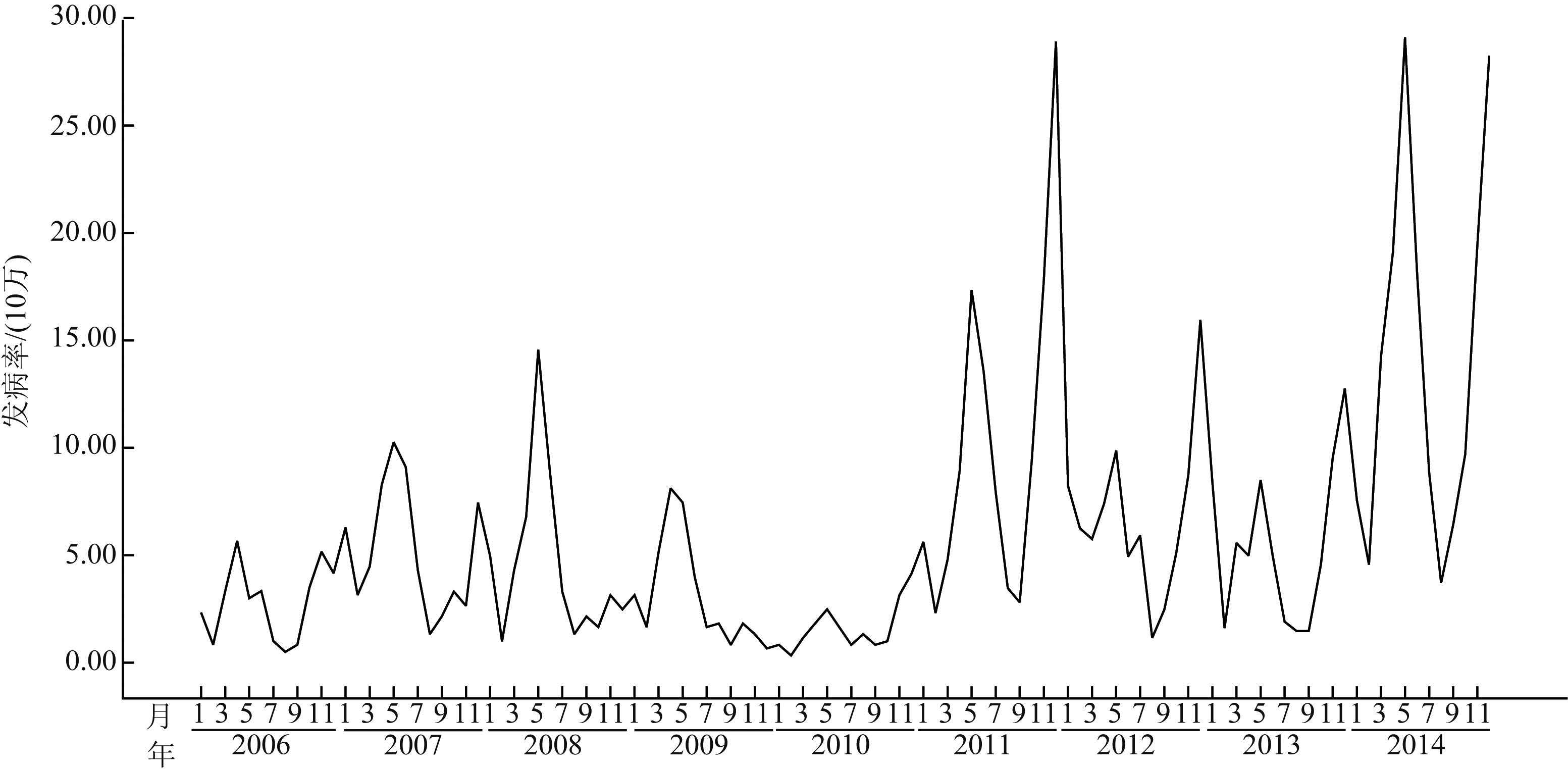
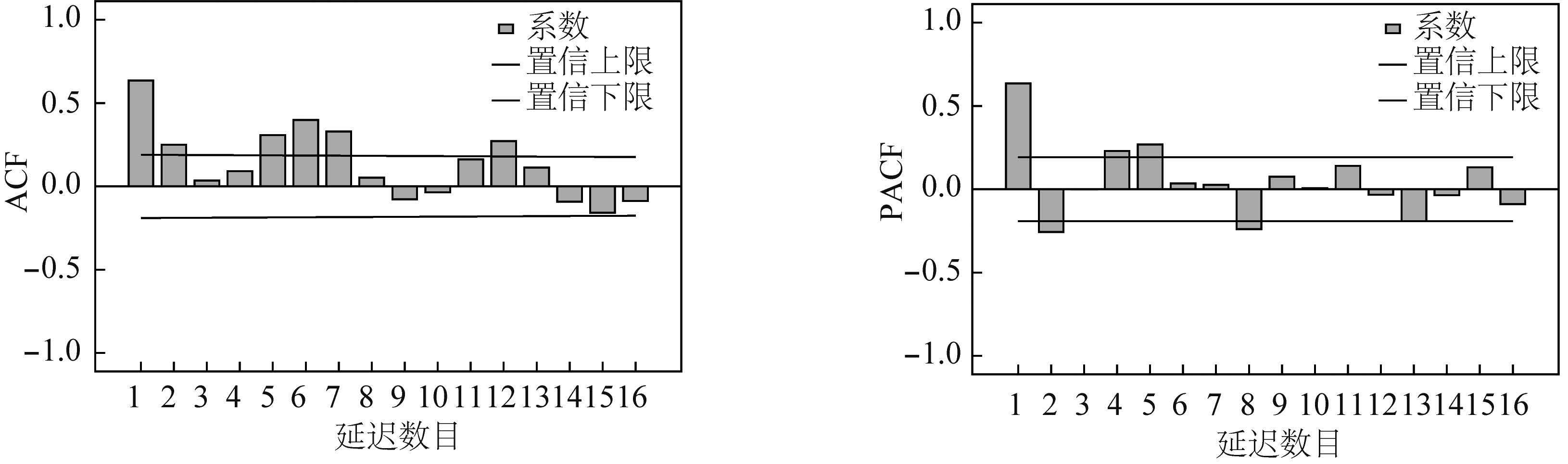
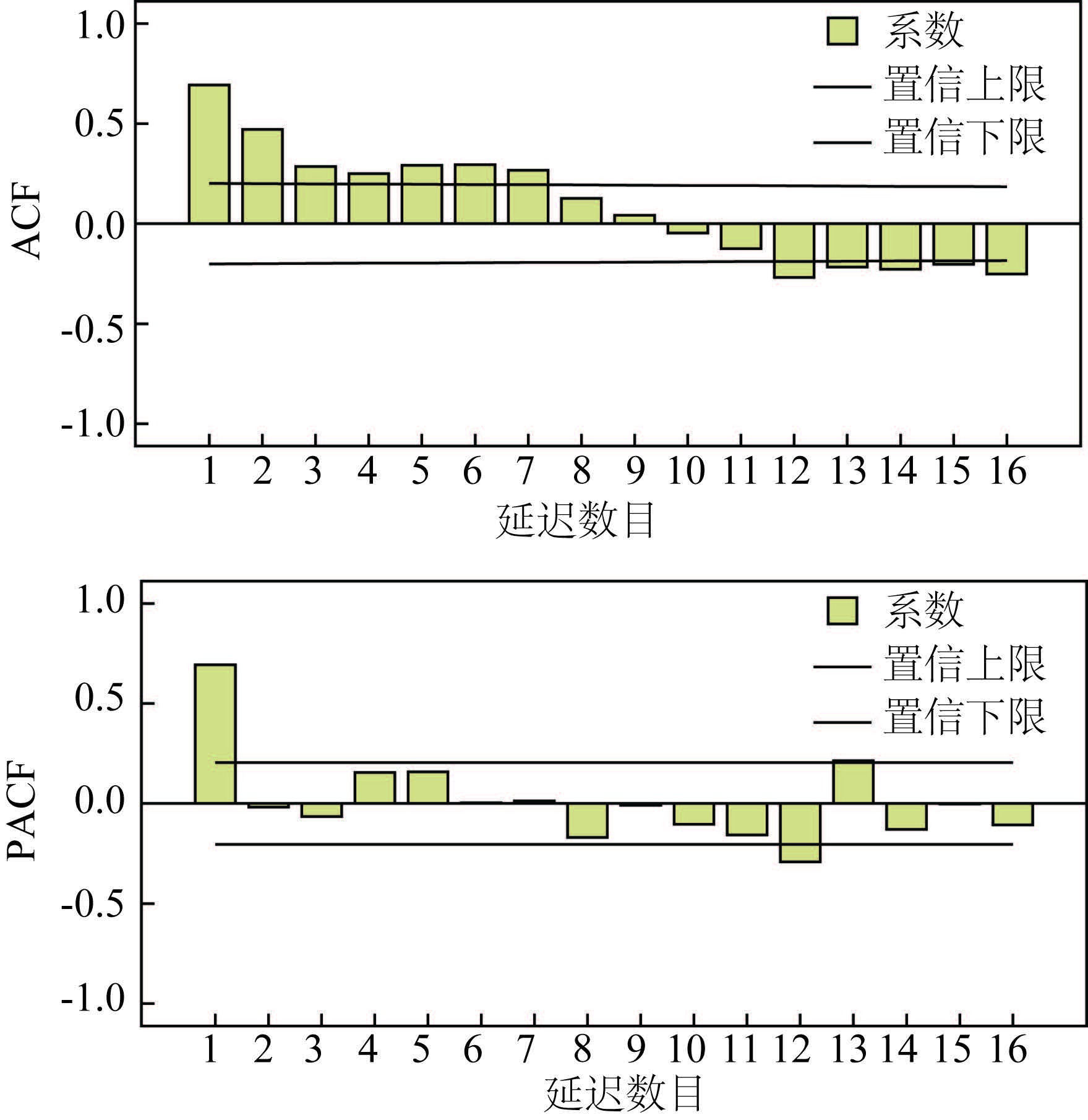
2 ARIMA模型的建立 2.1 模型识别

从2006-2014年济南市猩红热月发病率序列图(图 1)可以看出，发病率在2007年出现小高峰，2006-2010年基本处于平稳状态，2011年发病率急剧攀升，2013年回落，2014年又急剧升高；另外从猩红热月发病率的ACF、 PACF图(图 2)来看，自相关函数值下降为0后，又在5~7阶出现有意义，说明序列不平稳，季节周期性明显。通过ADF三个模型的检验t统计量均大于临界值，不拒绝零假设，认为数据不平稳。考虑对原始数列进行一阶季节性差分。经ADF检验t=-9.31＜-2.58(1%临界值)，拒绝零假设，认为不存在单位根，数据平稳。绘制猩红热月发病率一阶季节差分后的自相关系数、偏自相关系数图(图 3)。ACF拖尾，PACF截尾，以及从低阶到高阶逐个试验，对ARIMA(p,d,q)模型初步拟合，结果显示残差不是白噪声，模型拟合不理想，考虑该序列具有短期相关性又有季节效应，不能简单的、可加性的提取，假定短期相关性和季节性之间有乘积关系，尝试使用季节乘 积模型，认为值得进一步分析的模型有：(2,0,0)×(0,1,1)12、(1,0,0)×(0,1,1)12、(1,0,1)×(0,1,1)12、(2,0,1)×(0,1,1)12、(1,0,1)×(0,1,2)12。

图 1 2006-2014年济南市猩红热月发病率序列结果 Figure 1 Monthly incidence of scarlet fever in Jinan,2006-2014
图选项
图 2 原始序列猩红热月发病率ACF、PACF Figure 2 ACF and PACF of incidence of scarlet fever by month
图选项
图 3 原始序列一阶季节性差分后猩红热发病率的ACF、PACF Figure 3 ACF and PACF of incidence of scarlet fever by first-order seasonal difference
图选项
2.2 模型参数估计

通过对模型的拟合优度检验，根据BIC原则，得出模型(2,0,0)×(0,1,1)12、(1,0,0)×(0,1,1)12比较适合本次预测，见表 1。

表 1 各备选模型的拟合优度检验 Table 1 Test of goodness of fit of every alternative models
指标(2,0,0)×(0,1,1)12(1,0,0)×(0,1,1)12(1,0,1)×(0,1,1)12(2,0,1)×(0,1,1)12(1,0,1)×(0,1,2)12
R20.640.640.640.650.64
BIC2.792.732.792.892.85
表选项
2.3 模型诊断

(2,0,0)×(0,1,1)12模型R2为0.64，BIC为2.79；残差的ACF、PACF与Box-Ljung Q 为0.71(P=0.71)。(1,0,0)×(0,1,1)12模型R2为0.64，BIC为2.73，残差的ACF、PACF与Box-Ljung Q 为0.67(P=0.67),可知两模型的残差属于白噪声，两个模型均可以进行预测。对模型参数检验，得出(2,0,0)×(0,1,1)12模型的AR(2) 不太显著，结合各自R2,以及BIC最优原则，认为(1,0,0)×(0,1,1)12较好。通过用平均误差率(MER)及R2评价两个模型的效果，MER=平均误差绝对值/实际值均值，两个模型的MER分别是13.75%和13.86%，结合各自R2，可以看出模型(2,0,0)×(0,1,1)12的效果要略优于(1,0,0)×(0,1,1)12，见表 2。

表 2 (2,0,0)×(0,1,1)12、(1,0,0)×(0,1,1)12 模型的参数估计和假设检验 Table 2 Parameter estimation and hypothesis testing of model(2,0,0)×(0,1,1)12,(1,0,0)×(0,1,1)12
参数(2,0,0)×(0,1,1)12(1,0,0)×(0,1,1)12
BtpBtp
常数1.152.650.041.181.930.06
AR10.787.430.000.729.500.00
AR2-0.09-0.830.41---
SMA10.655.360.000.645.330.00
表选项
2.4 模型预测

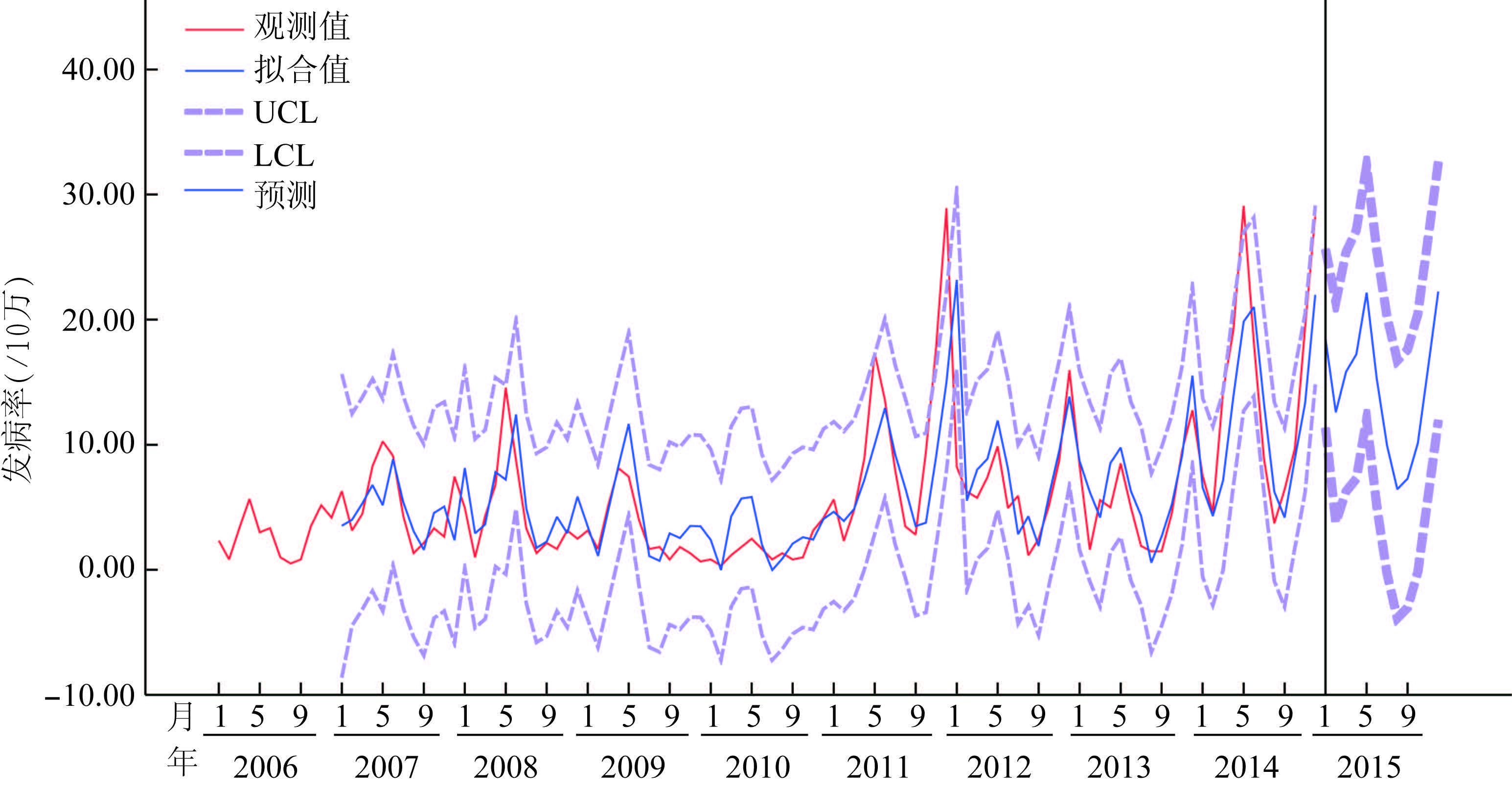
用模型回代预测2006-2014年猩红热月发病率和外推预测2015年猩红热发病率(图 4)，从预测结果分析，2006-2014年实际值和预测值趋势基本吻合，实际值稍高于预测值，接近置信区间的上限，提示2015年猩红热发病仍然处于较高水平，虽然与预测值不完全一样，但仍处于可信区间之内。预测1-6月的发病率分别为18.92/10万、12.15/10万、17.98/10万、19.54/10万、26.19/10万、17.24/10万。实际值分别为22.11/10万、11.27/10万、15.60/10万、13.41/10万、25.97/10万、22.11/10万。6月达到高峰随后下降，在11-12月将会升高，最低也会保持在5.00/10万以上。

图 4 (1,0,0)×(0,1,1)12模型拟合值和实测值比较 Figure 4 Comparison of model fitting values and actual values
图选项
3 讨论

ARIMA模型是一种传统的时间序列模型，在计量经济学上已经得到广泛应用，在传染病监测预警领域备受关注。综合考虑了序列的趋势变化，周期变化及随机误差，通过反复识别修改，直至获得满意的模型，操作过程简单方便，可以利用多种软件实现。ARIMA季节乘积模型更充分考虑时间序列的趋势变化、周期变化，将影响传染病发病的社会、自然、医学等因素的综合效应蕴含于时间变量中进行分析，适用于传染病的短期预测，实用性强、精度高[3]。既往研究中，ARIMA模型被广泛用于猩红热、细菌性痢疾、 甲型病毒性肝炎、乙型病毒性肝炎、流行性腮腺炎等传染病的预测，取得良好的预测效果[3, 5-10]。

从模型拟合的角度来看，ARIMA模型要求时间序列长度在30个数据以上，本研究利用2006-2014年共108个月的流行性腮腺炎月报告发病率的数据，建立ARIMA季节乘积模型，序列相对较长，该模型残差序列为白噪声，模型构建理想；资料分析结果显示，发病率拟合线和实际值曲线走势基本一致，外推预测2015年发病率与实际值比较，根据预测数据的可信限，实际发病率在预测值95%可信区间内波动，表明模型预测效果良好。

从预测结果来看，实际值高于预测值并且接近可信区间的上限，说明预测值和实际值的相对误差不够理想，预测精度有待进一步提高。 ARIMA 模型只能用于短期预测，单次分析建立的数学模型，不能作为永久不变的预测工具，在实际工作中，应不断加入新时间序列，对模型进行修正和重新拟合[8]，提示今后的工作中应及时加入新的时间序列，及时用新的数据进行修订，以提高模型的预测精度。此外，有研究发现组合模型可能预测精度更高，提示应深入探讨其他模型和组合模型对济南市猩红热发病率的探索应用，寻找更加适合于济南市猩红热发病预测的模型，从而提高预测的精度，为控制决策的制定提供强有力的数据支持[11-12]。

2006-2015年猩红热发病预测结果显示，2015年1-6月疫情基本稳定，全年呈现2个发病高峰，分别为4-6月和11-12月。2011、2014和2015年发病率较高，最近2年可以看出实际发病率要高于预测值，接近于置信区间的上限，提示2015年济南市猩红热仍处于高流行期，杨芬等[2]研究发现广东省猩红热2011年疫情上升明显，之后几年可能会继续持续处于猩红热高流行期，这一结果与该研究预测结果一致。疫情升高的原因可能是传染病流行中的Z-K现象、气温变化、人群中GAS带菌状况等因素的变化导致[1, 8]，2011年疫情升高以来，医生诊断意识提高、媒体报道增加、关注度升高，也是导致猩红热报告发病率升高的因素。济南市2015年猩红热仍然呈高位、平稳流行的趋势，未来一段时间应警惕出现猩红热流行和暴发的可能，在高发时间、高发地点做好猩红热的监测和应对工作，防止暴发流行。

参考文献
[1] Li LL, Jiang XH, Sui X, et al. Epidemiologic characteristics of scarlet fever in China,2005-2011[J]. Chinese Journal of Public Health,, 2012, 28 (6) : 826–827 .(in Chinese) 李雷雷, 蒋希宏, 隋霞, 等. 中国2005-2011年猩红热疫情流行病学分析[J]. 中国公共卫生,2012,28 (6) :826–827.
[2] Yang F, Zhong HJ, Hong T, et al. Incidence trendency and epidemiological characteristics of scarlet fever in Guangdong province, 1950-2011[J]. South China Journal of Preventive Medicine, 2013, 39 (1) : 1–5 .(in Chinese) 杨芬, 钟豪杰, 洪腾, 等. 广东省1950-2011年猩红热发病趋势变化及流行特征分析[J]. 华南预防医学,2013,39 (1) :1–5.
[3] 时照华.探索ARIMA模型在呼吸道传染病疫情预测中的应用[D].合肥:安徽医科大学,2013. Shi ZH. Application of ARIMA model in prediction of respiratory infectious disease[D].Hefei: Anhui Medical University,2013. (in Chinese)
[4] 杨维中. 传染病预警理论与实践[M]. 北京: 人民卫生出版社, 2012 . Yang WZ. Early warning of infectious disease theory and practice[M]. Beijing: People's Medical Publishing House, 2012 .
[5] 艾薇.ARIMA乘积季节模型在我国法定传染病甲乙类发病率预测中的应用[D].沈阳:中国医科大学,2012. Ai W. Application of ARIMA product seasonal model in forecasting incidence of Notifiable Infectious Diseases class A and B in China[D]. Shenyang: China Medical University,2012. (in Chinese)
[6] Lin JY, Guo ZQ. Prediction of epidemiological tendency of scarlet fever innanning by ARIMA model[J]. Journal of Preventive Medicine Information, 2012, 28 (3) : 191–193 .(in Chinese) 林健燕, 郭泽强. ARIMA模型预测南宁市猩红热发病趋势[J]. 预防医学情报杂志,2012,28 (3) :191–193.
[7] Shi ZH, Su H, Qin FY, et al. Application of ARIMA model in prediction of respiratory infectious disease[J]. Acta Universitatis Medicinalis Anhui, 2013, 48 (7) : 783–786 .(in Chinese) 时照华, 苏虹, 秦凤云, 等. ARIMA模型在常见呼吸道传染病疫情预测中的应用[J]. 安徽医科大学学报,2013,48 (7) :783–786.
[8] Ren H, Wang Y, Chen ML, et al. Study on the epidemiological characteristics and incidence trend of scarlet fever in Shanghai,2005-2012[J]. Chinese Journal of Epidemiology, 2013, 34 (7) : 706–710 .(in Chinese) 任宏, 王晔, 陈明亮, 等. 上海市2005-2012年猩红热流行特征和发病趋势分析[J]. 中华流行病学杂志,2013,34 (7) :706–710.
[9] Zhang JJ, Shen H, Liu JY, et al. Analysis and prediction on epidemiology tendency and prediction of scarlet fever in Xuhui district of Shanghai[J]. Chinese Primary Health Care, 2014, 28 (12) : 46–48 .(in Chinese) 张俊婕, 沈红, 刘景壹, 等. 上海市徐汇区猩红热流行趋势分析及预测[J]. 中国初级卫生保健,2014,28 (12) :46–48.
[10] 李丹.应用三种数学模型对传染病疫情进行预测和分布拟合[D].沈阳:中国医科大学,2005. Li D. Application of three mathematical models in predicting and fitting infectious disease[D]. Shenyang: China Medical University,2005. (in Chinese)
[11] Wu HC, Xu XQ, Wang Z, et al. Application of ARIMA model for estimating the Incidence of bacillary dysentery[J]. Zhejiang Journal of Preventive Medicine, 2012, 24 (1) : 14–16 .(in Chinese) 吴昊澄, 徐绪卿, 王臻, 等. 浙江省细菌性痢疾月发病率ARIMA模型建立及预测分析[J]. 浙江预防医学,2012,24 (1) :14–16.
[12] Zhu Y, Xia JL, Wang J. Comparison of predictive effect between the single auto regressive integrated moving average (ARIMA) model and the ARIMA-generalized regression neural network (GRNN) combination model on the incidence of scarlet fever[J]. Chinese Journal of Epidemiology, 2009, 30 (9) : 964–968 .(in Chinese) 朱玉, 夏结来, 王静. 单纯ARIMA模型和ARIMA-GRNN组合模型在猩红热发病率中的预测效果比较[J]. 中华流行病学杂志,2009,30 (9) :964–968.