扩展功能
文章信息
- 李峰, 陈胤忠, 徐士林, 陈国清, 杨长庆, 李长城, 金辉
- LI Feng, CHEN Yin-zhong, XU Shi-lin, CHEN Guo-qing, YANG Chang-qing, LI Chang-cheng, JIN Hui
- ARIMA乘积季节模型在盐城市手足口病疫情预测中的应用
- Application of ARIMA product seasonal model in predicting incidence of hand foot and mouth disease in Yancheng
- 疾病监测, 2016, 31(10): 864-869
- Disease Surveillance, 2016, 31(10): 864-869
- 10.3784/j.issn.1003-9961.2016.10.015
-
文章历史
- 收稿日期:2016-04-22
2. 东南大学公共卫生学院, 江苏 南京 210009
2. Southeast University Public Health College, Nanjing 210009, Jiangsu, China
手足口病(hand foot mouth disease,HFMD)是由肠道病毒引起的传染病,多发生于5岁以下儿童, < 3岁的年龄组发病率最高,可引起手、足和口腔等部位的疱疹,少数患儿可引起心肌炎、肺水肿和无菌性脑膜脑炎等并发症,个别重症患儿病情发展快,导致死亡,我国每年感染手足口病的患者累计超过万人[1-3]。引发手足口病的肠道病毒有多种型,其中以柯萨奇病毒A组16型(Cox A16)和肠道病毒71型(EV71)感染最为常见[4-6]。近年来,运用传染病动力学的数学模型预测传染病的流行趋势[7],为传染病的监测预警和控制提供了科学依据。用于传染病发病率预测研究的方法大体可以分为时间序列分析、人工神经网络和回归分析等,其中时间序列分析方法最受学者青睐[8]。而时间序列分析方法中,又以利用自回归移动平均(ARIMA)模型预测传染病的发病趋势较多,且取得很好的预测效果[9-12]。盐城市手足口病疫情占全市传染病发病率比重较大,为全市重点防控的主要传染病之一,利用这一资料建立时间序列模型,可以较好地对其发病进行预测,为盐城市手足口病的预防控制提供依据[13-14]。因此,本研究采用ARIMA乘积季节模型预测盐城市手足口病发病趋势,评价其预测性能,以探讨该方法进行手足口病预测预警的可行性。
1 资料与方法 1.1 资料来源数据资料来源于中国疾病预防控制信息系统,以现住详细地址在盐城市辖区内,发病日期在2009年1月1日至2015年12月31日期间,剔除重卡后的临床诊断病例或实验室确诊病例来统计手足口病发病数,以月为时间单位计算各年手足口病发病数;人口数据来源于盐城市统计局。
1.2 方法时间序列分析方法中,ARIMA模型又称Box-Jenkins模型,由自回归AR(p)、差分I(d)和移动平均MA(q)三部分组成,模型中p表示模型的自回归阶数、d表示非平稳资料转化为平稳资料的差分阶数、q表示模型移动平均阶数,表达式为A(p,d,q)。由于手足口病资料同时具有长期趋势、季节性、周期性、短期波动和不规则变动等特点,单纯利用ARIMA模型预测不能取得满意的效果。ARIMA乘积季节模型是依据一列随时间变化而又相互关联的动态数据建立的一种效果较好的分析方法,能够运用到盐城市手足口病发病趋势预测中[15]。其表达式为A(p,d,q)(P,D,Q)s,其中s为季节周期,建模过程按以下阶段进行。
1.2.1 序列特征及平稳化应用时间序列图、自相关系数函数图(ACF)、偏自相关系数函数图(PACF)分析序列特征(趋势性、季节性),并利用单位根检验方法检验序列的平稳性。若序列平稳,进行平稳序列的时间序列分析;若序列不平稳,结合本文序列特征,采用普通差分和季节性差分等合适的数据预处理方法,实现序列平稳化后进行分析。
1.2.2 模型的识别根据ACF、PACF和SPSS模型拟合结果,如果平稳序列的自相关函数是拖尾的,偏相关函数是截尾的,即ACF随着滞后期的增加,函数值呈现指数或正弦波衰减,趋向于0,而PACF中函数值在某个滞后期后全部为0或全部收敛在置信区间内近似为0,则可确定序列有AR过程;如果平稳序列的自相关函数是截尾的,偏相关函数是拖尾的,则可确定序列有MA过程;如果平稳序列的自相关函数和偏相关函数均是拖尾的,则可确定序列有ARIMA过程。以此进行模型的初步识别和定阶。
1.2.3 参数估计和模型诊断利用非线性最小二乘法估计模型参数。参数估计后,对模型的残差序列进行白噪声检验,用以判断模型的适合性。对于残差而言相互独立就为白噪声,原假设为数据是相互独立分布的,如果P值足够大则接受原假设,认为残差相互独立,为随机性误差,说明ARIMA模型比较适合,不需要重新选择模型。依据标准化贝叶斯信息准则(Normalized BIC)确定模型阶数,如不恰当则返回第二阶段,重新选定模型。通过不断改变模型的阶数并调试比较,确定残差序列为白噪声,Normalized BIC值最小且模型较为简洁的为最佳模型[10]。
1.2.4 模型校验与预测根据已建立的ARIMA乘积季节模型拟合2010年1月至2015年6月的手足口病发病率,通过观察模型拟合序列图和计算模型拟合误差,检验模型的拟合效果。利用此模型进一步预测2015年7—12月手足口病发病率,通过计算模型预测误差对模型的预测能力进行校验,若模型拟合预测能力达不到预期效果,需校正模型,最后以校正后的模型对盐城市2016年手足口病发病率进行预测。
1.3 统计学分析采用Excel 2010、SPSS 16.0软件进行数据存储和管理,SPSS 16.0、EViews 5软件对数据资料进行统计分析[16]。
2 结果 2.1 序列的特征及平稳化选取2009年1月至2015年6月的78个数据绘制序列图(图 1),可以看出2009年1月至2015年6月期间,盐城市手足口病发病率有逐年上升的趋势,发病率序列为非平稳序列。为此,需要对发病率数据进行对数转换。
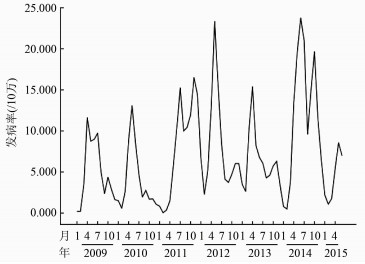
|
| 图 1 2009年1月至2015年6月盐城市手足口病月发病率 Figure 1 Incidence series of HFMD in Yancheng, January 2009-June 2015 |
| |
发病率序列经对数变换后,从季节性因素分解表可见(表 1),手足口病发病率呈明显季节规律,4-7月达到高峰,由此需对序列进行季节差分。根据手足口病季节性发病的特点,选取季节周期s为12,建立ARIMA乘积季节模型。
| 月份 | 季节性因素(%) |
| 1 | 36.207 |
| 2 | 13.350 |
| 3 | 51.343 |
| 4 | 159.144 |
| 5 | 187.935 |
| 6 | 183.567 |
| 月份 | 季节性因素(%) |
| 7 | 152.906 |
| 8 | 78.564 |
| 9 | 82.033 |
| 10 | 99.849 |
| 11 | 92.256 |
| 12 | 62.848 |
对数变换及季节性差分后,利用EViews 5中单位根检验方法来检验序列的平稳性,得到Augmented Dickey-Fuller检验统计量t=-7.002(P < 0.05),序列平稳,可以确定模型中d=0,D=1。
2.2 模型的识别发病率序列经对数转换和一阶季节差分后,序列作自相关系数ACF和偏相关系数PACF(图 2),ACF在季节时点1、12和36处呈指数衰减,趋向于0,ACF有个拖尾。而PACF在时点1以后,偏相关系数基本收敛在置信区间内,近似截尾,提示季节性模型A(P,D,Q)12有AR过程,且P=1已满足建模要求[16]。
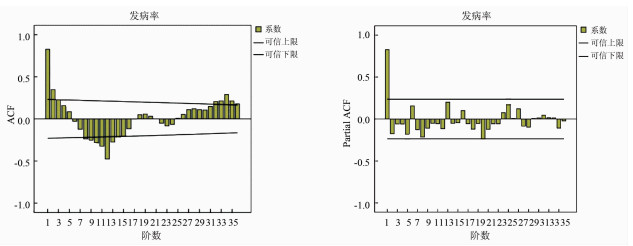
|
| 图 2 对数变化后一阶季节性差分ACF和PACF Figure 2 ACF and PACF of first-order difference of incidence series after natural log transform |
| |
正确识别季节性模型后,取P=1,Q=0,绘制季节性模型A(1,1,0)12的残差序列ACF和PACF,残差序列ACF和PACF均有拖尾,提示非季节模型A(p,d,q)有ARMA过程,且p、q都不超过2阶,分别取p=1、2和q=1、2,建立ARIMA乘积季节模型A(1,0,1)(1,1,0)12、A(2,0,1)(1,1,0)12和A(1,0,2)(1,1,0)12、A(2,0,2)(1,1,0)12。
2.3 模型参数估计和模型诊断利用SPSS16.0软件分析,给出4个模型的参数估计(表 2)和拟合优度检验结果(表 3)。观察模型的参数估计,模型A(1,0,1)(1,1,0)12中除了常数项,各参数估计均具有统计学意义(P < 0.05),再观察拟合优度检验中Ljung-Box统计量,四个模型残差序列基本属于白噪声序列(P > 0.05),最后依据标准化贝叶斯信息准则(Normalized BIC),Normalized BIC值最小且模型较为简洁的为最佳模型,最终选定模型A(1,0,1)(1,1,0)12(Normalized BIC值为2.997)。
| 参数 | A(1, 0, 1)(1, 1, 0)12 | A(2, 0, 1)(1, 1, 0)12 | A(1, 0, 2)(1, 1, 0)12 | A(2, 0, 2)(1, 1, 0)12 | |||||||||||
| B | t | P | B | t | P | B | t | P | B | t | P | ||||
| AR1 | 0.569 | 4.258 | 0.000 | 0.486 | 1.335 | 0.187 | 0.652 | 3.020 | 0.004 | 1.566 | 10.653 | 0.000 | |||
| AR2 | - | - | - | 0.079 | 0.026 | 0.796 | - | - | - | -0.626 | -4.864 | 0.000 | |||
| MA1 | -0.445 | -3.001 | 0.004 | -0.517 | -1.542 | 0.128 | -0.344 | -1.340 | 0.185 | 0.609 | 0.047 | 0.963 | |||
| MA2 | - | - | - | - | - | - | 0.093 | 0.396 | 0.694 | 0.391 | 0.076 | 0.940 | |||
| SAR1 | -0.565 | -4.841 | 0.000 | -0.566 | -4.471 | 0.000 | -0.567 | -4.749 | 0.000 | -0.551 | -4.636 | 0.000 | |||
| 常数 | 0.649 | 0.608 | 0.545 | 0.637 | 0.572 | 0.569 | 0.662 | 0.541 | 0.590 | 0.867 | 1.482 | 0.144 | |||
| 模型 | Normalized BIC |
Ljung-Box 值 |
Ljung-Box (P值) |
| A(1, 0, 1)(1, 1, 0)12 | 2.997 | 20.692 | 0.147 |
| A(2, 0, 1)(1, 1, 0)12 | 3.075 | 20.883 | 0.106 |
| A(1, 0, 2)(1, 1, 0)12 | 3.073 | 29.312 | 0.102 |
| A(2, 0, 2)(1, 1, 0)12 | 3.114 | 58.715 | 0.102 |
利用模型A(1,0,1)(1,1,0)12拟合盐城市2010年1月至2015年6月的手足口病发病率,绘制拟合序列图,可见模型能够较好地拟合出手足口病发病率高峰和低谷,接近实际发病率趋势,且实际值都在拟合值的95%可信上限内,模型拟合效果较好(图 3)。比较模型拟合值与实际值,除极端值外,模型拟合的相对误差基本集中在50%以下,去除极端值后,平均误差率为41.296%,模型精度不高。利用模型进一步预测2015年7—12月的发病率,比较预测值与发病率(表 4),模型预测的平均误差率为23.998%,模型的预测精度高于拟合精度。总体来看,A(1,0,1)(1,1,0)12模型具有一定的发病率拟合预测能力。
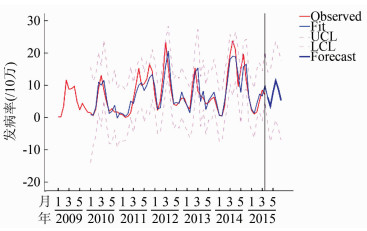
|
| 图 3 A(1,0,1)(1,1,0)12模型拟合结果Figure Figure 3 of A(1, 0, 1)(1, 1, 0)12model |
| |
| 时间(月) | 预测值 (/10万) |
实际值 (/10万) |
相对误差 (/10万) |
| 7 | 6.317 | 6.706 | 5.801 |
| 8 | 3.484 | 2.608 | 33.589 |
| 9 | 7.792 | 6.47 | 20.433 |
| 10 | 11.466 | 10.588 | 8.292 |
| 11 | 8.822 | 6.141 | 43.657 |
| 12 | 5.285 | 7.797 | 32.218 |
| 平均误差 | 23.998 |
应用模型A(1,0,1)(1,1,0)12预测盐城市2016年手足口病发病率(表 5),为早期预警防控手足口病流行提供依据。
| 时间(月) | 预测值(/10万) |
| 1 | 2.178 |
| 2 | 1.631 |
| 3 | 3.807 |
| 4 | 10.910 |
| 5 | 15.796 |
| 6 | 17.460 |
| 7 | 15.613 |
| 8 | 7.952 |
| 9 | 12.877 |
| 10 | 17.103 |
| 11 | 11.357 |
| 12 | 6.935 |
手足口病病原学复杂,传染力强,极易在托幼机构中造成暴发流行。影响该病发生的因素较多,有报道称手足口病与儿童职业(托幼儿童、散居儿童)、卫生习惯、家庭经济情况,城乡居住地等因素有关[17-18]。时间序列分析作为传统的线性模型分析手段,克服了影响预测对象的因素、不易分析和数据资料不易得到等难题,具有以时间变量综合代替各影响因素,不需要知道影响结局变量相关因素的优点。ARIMA模型作为时间序列分析中的经典模型,是时间序列分析中较为成熟和应用较为广泛的方法之一,而ARIMA乘积季节模型又是一种能够充分考虑资料可能同时具有长期趋势、季节性、周期性、短期波动和不规则变动等数据特点而建立的一种效果较好的分析方法,具有建模过程简单、经济、适用,短期预测精度较高等优点,广泛应用于传染病发病率的预测[8, 19-20]。
本研究利用盐城市2009-2015年手足口病网络监测发病数据,考虑到手足口病的季节周期性特点,采用ARIMA乘积季节模型拟合预测手足口病发病率,满足7~8个周期量的要求[10],经对数变换、季节差分使数据平稳,根据拟合优度检验和残差白噪声检验最终模型为A(1,0,1)(1,1,0)12,其拟合值与实际值比较接近,实际值均在拟合值的95%可信上限内,利用2015年7—12月的发病率数据检验模型的预测效果,模型预测平均误差率为23.998%,查阅相关文献[9, 12, 21],可认为该模型适合对盐城市2016年的手足口病发病率进行预测。同时,还可通过预测值的95%可信区间来判断实际发病率是否在正常范围内波动,如果实际发病率在预测值95%可信区间范围内,表明当月疫情基本正常,反之应警惕手足口病暴发或流行的可能[21]。该模型可对指导盐城市手足口病疫情的监测预警和预防控制工作提供科学的理论依据。
本研究结果还显示,模型A(1,0,1)(1,1,0)12拟合值和实际值的平均误差率为41.296%,误差较大,模型预测的精确度有待进一步提高。分析其原因,表明模型拟合相对误差存在极端值,可能与该市手足口病疫情监测数据质量不高有关。而监测数据稳定性不高,可能会降低该模型的预测效率。此外,影响手足口病发病的危险因素错综复杂,很多因素未被考虑到模型参数中,也可能会影响模型的精确度,有待今后进一步研究探讨。胡跃华等[12]利用ARIMA模型预测全国手足口病发病率的平均相对误差为0.52,姚英和沈毅[21]利用ARIMA模型预测手足口病发病率的相对误差为28.80%,说明单纯利用ARIMA模型预测手足口病发病率存在预测精度不高的问题,如果能在尽可能控制影响因素的情况下再组合使用ARIMA模型和其他预测方法[22],例如ARIMA-GRNN模型[8],模型预测效果可能会更理想。
作者贡献:李峰:数据的处理、分析,模型的建立,论文的撰写。
陈胤忠、金辉:技术指导
徐士林、陈国清、杨长庆、李长城:数据收集、整理
| [1] | Yang SJ, Li LJ, Ren H, et al. Infectious diseases[M].8th ed. Beijing: People's Medical Publishing House, 2013 : 125 -130. (in Chinese) 杨绍基, 李兰娟, 任红, 等. 传染病学[M].8版. 北京: 人民卫生出版社, 2013 : 125 -130. |
| [2] | Hu YH, Xiao GX, Guo Y, et al. The epidemic features of hand, foot, mouth disease during 2008-2011 in China[J]. Chinese Journal of Disease Control and Prevention , 2014, 18 (8) : 693–697. (in Chinese) 胡跃华, 肖革新, 郭莹, 等. 2008-2011年中国大陆手足口病流行特征分析[J]. 中华疾病控制杂志 , 2014, 18 (8) : 693–697. |
| [3] | Soto SM. Human migration and infectious diseases[J]. Clin Microbiol Infect , 2009, 15 (Suppl 1) : S26–28. |
| [4] | Li XT, Liu BW, Jia L, et al. Study on the risk factors of hand-foot-mouth disease deaths in Beijing, 2010[J]. Chinese Journal of Disease Control and Prevention , 2012, 16 (5) : 408–411. (in Chinese) 李锡太, 刘白薇, 贾蕾, 等. 北京市2010年手足口病死亡危险因素分析[J]. 中华疾病控制杂志 , 2012, 16 (5) : 408–411. |
| [5] | Sui ML, Zhang C, Huang XY, et al. Etiology, clinical characteristics, and laboratory results in patients with severe hand, foot, mouth disease[J]. Journal of Pathogen Biology , 2015, 10 (6) : 481–486. (in Chinese) 隋美丽, 张超, 黄学勇, 等. 重症手足口病病原学与临床特征及实验室指标的关系研究[J]. 中国病原生物学杂志 , 2015, 10 (6) : 481–486. |
| [6] | Feng HF, Duan GC, Zhang RG, et al. Time series analysis hand-foot-mouth disease hospitalization in Zhengzhou:establishment of forecasting models using climate variables as predictors[J]. PLoS One , 2014, 9 (1) : e87916. DOI:10.1371/journal.pone.0087916 |
| [7] | Ma ZE, Zhou YC, Wang WD, et al. Modeling and dynamics of infectious diseases[M]. Beijing: Science Press, 2004 . (in Chinese) 马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004 . |
| [8] | Wang ZL, Hu YH. Applied time series analysis[M]. Beijing: Science Press, 2007 . (in Chinese) 王振龙, 胡永宏. 应用时间序列分析[M]. 北京: 科学出版社, 2007 . |
| [9] | Wu JB, Ye LX, You EK. Prediction of incidence of notifiable contagious diseases by appalication of time series model[J]. Journal of Mathematical Medicine , 2007, 20 (1) : 90–92. (in Chinese) 吴家兵, 叶临湘, 尤尔科. ARIMA模型在传染病发病率预测中的应用[J]. 数理医药学杂志 , 2007, 20 (1) : 90–92. |
| [10] | Peng ZH, Bao CJ, Zhao Y, et al. ARIMA product season model and its application on forecasting in incidence of infectious disease[J]. Application of Statistics and Management , 2008, 27 (2) : 362–368. (in Chinese) 彭志行, 鲍昌俊, 赵杨, 等. ARIMA乘积季节模型及其在传染病发病预测中的应用[J]. 数理统计与管理 , 2008, 27 (2) : 362–368. |
| [11] | Pan H, Hu JY, Wu HY, et al. Comparison of GM(1, 1)gray model and ARIMA model in forecasting the incidence of hand-foot-mouth disease in Shanghai[J]. Chinese Journal of Disease Control and Prevention , 2011, 15 (5) : 445–448. (in Chinese) 潘浩, 胡家瑜, 吴寰宇, 等. GM(1, 1)灰色模型和ARIMA模型在上海市手足口病发病率预测应用中的比较研究[J]. 中华疾病控制杂志 , 2011, 15 (5) : 445–448. |
| [12] | Hu YH, Liao JQ, Feng GS, et al. Application of multiple seasonal autoregressive integrated moving average model in prediction of incidence of hand foot and mouth disease in China[J]. Disease Surveillance , 2014, 29 (10) : 827–832. (in Chinese) 胡跃华, 廖家强, 冯国双, 等. 自回归移动平均模型在全国手足口病疫情预测中的应用[J]. 疾病监测 , 2014, 29 (10) : 827–832. |
| [13] | Wu HC, Xu XQ, Wang Z, et al. Application of ARIMA model for estimating the incidence of bacillary dysentery[J]. Zhejiang Journal of Preventive Medicine , 2012, 24 (1) : 14–16. (in Chinese) 吴昊澄, 徐旭卿, 王臻, 等. 浙江省细菌性痢疾月发病率ARIMA模型建立及预测分析[J]. 浙江预防医学 , 2012, 24 (1) : 14–16. |
| [14] | Yang Z, Ye ZH, You AG, et al. Application of multiple seasonal ARIMA model in prediction of tuberculosis incidence[J]. Chinese Journal of Public Health , 2013, 29 (4) : 469–472. (in Chinese) 杨召, 叶中辉, 尤爱国, 等. 乘积季节ARIMA模型在结核病发病率预测中的应用[J]. 中国公共卫生 , 2013, 29 (4) : 469–472. |
| [15] | Xiang LH, Guo ZP, Yang XT, et al. Research progress of statistical forecasting on morbidity tendency of infectious diseases[J]. Strait Journal of Preventive Medicine , 2010, 16 (6) : 27–29. (in Chinese) 向伦辉, 郭祖鹏, 杨兴堂, 等. 传染病发病趋势常见统计预测方法的研究进展[J]. 海峡预防医学杂志 , 2010, 16 (6) : 27–29. |
| [16] | Zhang WT. Advanced tutorial of SPSS[M]. Beijing: Beijing Hope Electronic Press, 2002 : 277 -285. (in Chinese) 张文彤. SPSS11统计分析教程(高级篇)[M]. 北京: 北京希望电子出版社, 2002 : 277 -285. |
| [17] | Li L, Xu K, Qi X, et al. Risk factors of hand-foot-mouth disease among children[J]. Chinese Journal of Public Health , 2011, 27 (1) : 16–18. (in Chinese) 李亮, 许可, 祁贤, 等. 儿童手足口病影响因素病例对照研究[J]. 中国公共卫生 , 2011, 27 (1) : 16–18. |
| [18] | Zhu WP, Xue CY, Shen DX, et al. Investigation and analysis on epidemiology and effect factors of hand-foot-mouth disease in Pudong New Area of Shanghai[J]. Maternal and Child Health Care of China , 2010, 25 (17) : 2401–2403. (in Chinese) 朱渭萍, 薛曹怡, 沈迪莘, 等. 上海市浦东新区手足口病流行病学调查及影响因素分析[J]. 中国妇幼保健 , 2010, 25 (17) : 2401–2403. |
| [19] | Ubeyli ED, Güler I. Spectral analysis of internal carotid arterial Doppler signals using FFT, AR, MA, and ARMA methods[J]. Comput Biol Med , 2004, 34 (4) : 293–306. DOI:10.1016/S0010-4825(03)00060-X |
| [20] | Lan YJ, Shen GA, Li H, et al. Time analysis and forecasting of Sichuan province pneumoconiosis[J]. Journal of Occupational Health and Damage , 2001, 16 (4) : 204–206. (in Chinese) 兰亚佳, 沈国安, 李宏, 等. 四川省尘肺病时间趋势分析与预测[J]. 职业卫生与病防 , 2001, 16 (4) : 204–206. |
| [21] | Yao Y, Shen Y. The application of ARIMA model in predicting incidence trend of hand-foot-mouth disease[J]. Zhejiang Journal of Preventive Medicine , 2015, 27 (2) : 147–149. (in Chinese) 姚英, 沈毅. 手足口病发病趋势的ARIMA模型预测[J]. 浙江预防医学 , 2015, 27 (2) : 147–149. |
| [22] | Hu JL, Liu WD, Liang Q, et al. Applications of season index method and ARIMA model on weekly prediction of infectious diarrhea incidence[J]. Chinese Journal of Disease Control and Prevention , 2013, 17 (8) : 718–721. (in Chinese) 胡建利, 刘文东, 梁祁, 等. 季节指数法和ARIMA模型在感染性腹泻周发病数预测中的应用研究[J]. 中华疾病控制杂志 , 2013, 17 (8) : 718–721. |
 2016, Vol. 31
2016, Vol. 31


